Question

A catapult launches a test rocket vertically upward from a well, giving the rocket an initial speed of 80.6 m/s at ground level. The engines then fire, and the rocket accelerates upward at 3.90 m/s2 until it reaches an altitude of 1150 m. At that point its engines fail, and the rocket goes into free fall, with an acceleration of ?9.80 m/s2. (You will need to consider the motion while the engine is operating and the free-fall motion separately.)

(a) For what time interval is the rocket in motion above the ground?
(b) What is its maximum altitude?
(c) What is its velocity just before it hits the ground?

Answer 1

Before the engines fail, the rocket's altitude at time t is given by

`y_1(t)=\left(80.6(\rm m)/(\rm s)\right)t+\frac12\left(3.90(\rm m)/(\mathrm s^2)\right)t^2`

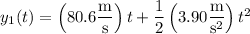
and its velocity is

`v_1(t)=80.6(\rm m)/(\rm s)+\left(3.90(\rm m)/(\mathrm s^2)\right)t`

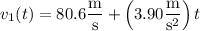
The rocket then reaches an altitude of 1150 m at time t such that

`1150\,\mathrm m=\left(80.6(\rm m)/(\rm s)\right)t+\frac12\left(3.90(\rm m)/(\mathrm s^2)\right)t^2`

Solve for t to find this time to be

`t=11.2\,\mathrm s`

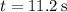
At this time, the rocket attains a velocity of

`v_1(11.2\,\mathrm s)=124(\rm m)/(\rm s)`

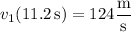
When it's in freefall, the rocket's altitude is given by

`y_2(t)=1150\,\mathrm m+\left(124(\rm m)/(\rm s)\right)t-\frac g2t^2`

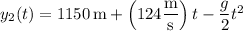
where
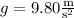`g=9.80(\rm m)/(\mathrm s^2)` is the acceleration due to gravity, and its velocity is

`v_2(t)=124(\rm m)/(\rm s)-gt`

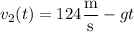
(a) After the first 11.2 s of flight, the rocket is in the air for as long as it takes for
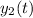`y_2(t)` to reach 0:

`1150\,\mathrm m+\left(124(\rm m)/(\rm s)\right)t-\frac g2t^2=0\implies t=32.6\,\mathrm s`

So the rocket is in motion for a total of 11.2 s + 32.6 s = 43.4 s.

(b) Recall that

`{v_f}^2-{v_i}^2=2a\Delta y`

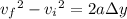
where
`v_f` and
`v_i` denote final and initial velocities, respecitively,
`a` denotes acceleration, and
`\Delta y` the difference in altitudes over some time interval. At its maximum height, the rocket has zero velocity. After the engines fail, the rocket will keep moving upward for a little while before it starts to fall to the ground, which means
`y_2` will contain the information we need to find the maximum height.

`-\left(124(\rm m)/(\rm s)\right)^2=-2g(y_(\rm max)-1150\,\mathrm m)`

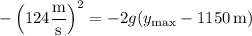
Solve for
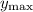`y_(\rm max)` and we find that the rocket reaches a maximum altitude of about 1930 m.

(c) In part (a), we found the time it takes for the rocket to hit the ground (relative to
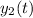`y_2(t)`) to be about 32.6 s. Plug this into
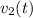`v_2(t)` to find the velocity before it crashes:

`v_2(32.6\,\mathrm s)=-196(\rm m)/(\rm s)`

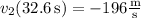
That is, the rocket has a velocity of 196 m/s in the downward direction as it hits the ground.