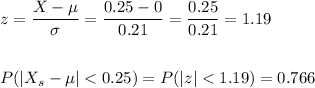Question

In an analysis of healthcare data, ages have been rounded to the nearest multiple of 5 years. The difference between the true age and the rounded age is assumed to be uniformly distributed on the interval from -2.5yrs to +2.5yrs. The healthcare data are based on a random sample of 48 people.What is the approximate probability that the mean of the rounded ages within 0.25 years of the mean of the true ages?

Answer 1

The approximate probability that the mean of the rounded ages within 0.25 years of the mean of the true ages is P=0.766.

Explanation:

We have a uniform distribution from which we are taking a sample of size n=48. We have to determine the sampling distribution and calculate the probability of getting a sample within 0.25 years of the mean of the true ages.

The mean of the uniform distribution is:

`\mu=(Max+Min)/(2)=(2.5+(-2.5))/(2)=0`

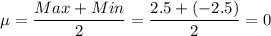
The standard deviation of the uniform distribution is:

`\sigma=(Max-Min)/(√(12))=(2.5-(-2.5))/(√(12))=(5)/(3.46)=1.44`

The sampling distribution can be approximated as a normal distribution with the following parameters:

`\mu_s=\mu=0\\\\\sigma_s=(\sigma)/(√(n))=(1.44)/(√(48))=(1.44)/(6.93)=0.21`

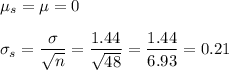
We can now calculate the probability that the sample mean falls within 0.25 from the mean of the true ages using the z-score:

`z=(X-\mu)/(\sigma)=(0.25-0)/(0.21)=(0.25)/(0.21)=1.19\\\\\\P(|X_s-\mu|<0.25)=P(|z|<1.19)=0.766`