Question

The container of a breakfast cereal usually lists the number of calories and the amounts of protein, carbohydrate, and fat contained in one serving of the cereal. The amounts for two common cereals are given below. Suppose a mixture of these two cereals is to be prepared that contains exactly 295 calories, 9 g of protein, 48 g of carbohydrate, and 8 g of fat.

a. Set up a vector equation for this problem. Include a statement of what the variables in your equation represent.
b. Write an equivalent matrix equation, and then determine if the desired mixture of the two cereals can be prepared.
$$\begin{matrix}
\text{Nutrient} & \text{General Mills Cherrios} & \text{Quaker 100% Natura Cereal}\
\text{Calories} & \text{110} & \text{130}\
\text{Protein (g)} & \text{4} & \text{3}\
\text{Carbhydrate (g)} & \text{20} & \text{18}\
\text{Fat (g)} & \text{2} & \text{5}\
\end{matrix}$$

Answer 1

(a)

`\left[\begin{array}{ccc}110\\4\\20\\2\end{array}\right] x+\left[\begin{array}{ccc}130\\3\\18\\5\end{array}\right] y=\left[\begin{array}{ccc}295\\9\\48\\8\end{array}\right]`

(b)

`\left[\begin{array}{ccc}110&130&295\\4&3&9\\20&18&48\\2&5&8\end{array}\right]`

1.5 servings of cheerios and 1 serving of Quaker 100% natural cereal will give the desired mixture.

Explanation:

Given the mixture of cereals below:

`\left|\begin{array}c&$General Mills &$Quaker \\$Nutrient&$Cherrios &100\% $Natural Cereal\\----&---&---\\$Calories&110&130\\$Protein (g)&4&3\\$Carbhydrate (g)&20&18\\$Fat (g)&2&5\end{array}\right|`

Suppose a mixture of these two portions of cereals is to be prepared that contain exactly 295 calories, 9 g of protein, 48 g of carbohydrate, and 8 g of fat.

(a)Let x be the number of servings of Cheerios

Let y be the number of servings of Natural Cereal

From the table above, we have

`110x+130y=295\\4x+3y=9\\20x+18y=48\\2x+5y=8`

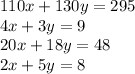
Then a vector equation for this problem is:

`\left[\begin{array}{ccc}110\\4\\20\\2\end{array}\right] x+\left[\begin{array}{ccc}130\\3\\18\\5\end{array}\right] y=\left[\begin{array}{ccc}295\\9\\48\\8\end{array}\right]`

(b) Next, we obtain an equivalent matrix equation of the data

`\left[\begin{array}{ccc}110&130\\4&3\\20&18\\2&5\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] =\left[\begin{array}{ccc}295\\9\\48\\8\end{array}\right]`

This is of the form AX=B. To solve for X we, therefore have an equivalence matrix:

`\left[\begin{array}{ccc}110&130&295\\4&3&9\\20&18&48\\2&5&8\end{array}\right]`

Next, we row reduce the matrix using a calculator to obtain the matrix:

`\left[\begin{array}{ccc}1&0&1.5\\0&1&1\\0&0&0\\0&0&0\end{array}\right]`

Therefore:

1x+0=1.5

0x+y=1

x=1.5 and y=1

To get the required mixture, we use 1.5 servings of cheerios and 1 serving of Quaker 100% natural cereal.