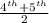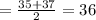Question

Which pair of numbers, if included in this set, would not change the median?

Answer 1

Option A

Explanation:

Given set is first arranged in ascending order

So, { 27, 28, 35, 37, 43, 47}

The numbers of observations (n) = 6

Since n is an even no.

Median =

`\frac{ { (n)/(2) }^(th) + { \: ((n)/(2) + 1)}^(th) observation}{2}`

`\frac{ {3}^(th) + {4}^(th) }{2}`

`= (35 + 37)/(2) = 36`

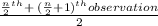
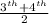
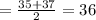
If we take the pair (35, 50)

and arrange them in the set

{ 27, 28, 35, 35,37, 43, 47,50}

No.s of observations = 8

So, Median=

`\frac{ {4}^(th) + {5}^(th) }{2}`

`= (35 + 37)/(2) = 36`

Answer 2

A)

Explanation:

Order the set first

27, 28, 35, 37, 43, 47

Median now is: 36 (which is the mean between 35 and 37, the two central numbers )

If you add A) 35,50 then you will still have to compute the mean between 35 and 37 in order to find the median, because you have:

27,28,35,35,37,43,47,50