Answer:
The perimeter of the shape is 28.13 cm
Explanation:
First of all, we will have to draw a line from point A to point C. This will divide the shape into two parts, both of which are triangles.
We will use the dimensions of the newly formed triangle ABC to get the side AC.
The cosine formula will be apt for this purpose:
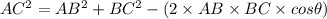
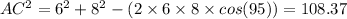
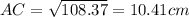
Now we have AC as 10.41 cm,
we can see that AC forms the hypothenuse of the right-angled triangle ADC.
From Pythagoras' theorem, DC can be calculated as
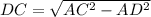
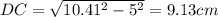
Therefore the perimeter of the shape is 8 + 5 + 9.13 + 6 =28.13 cm
The perimeter of the shape is 28.13 cm