Question

A local company is concerned about the number of days missed by its employees due to ill ness. A Random Sample of 10 employees is selected. The Number of days absent in one year is listed below. An Incentive program is offered in an attempt to decrease the number of days absent. The number of days ansent in one year after the incentive program is listed below. Test the claim that the incentive program cuts down on the number of days missed by employees. Use a=0.05. Assume that the distribution is normally distributied.

Employee A B C D E F G H I J
Days Absent Before incentive 3 8 7 2 9 4 2 0 7 5
Days absent after incentive 1 7 7 0 8 2 0 1 5 5

Answer 1

The new incentive program cuts down on the number of days missed by employees.

Explanation:

In this case we need to test whether the new incentive program cuts down on the number of days missed by employees.

The hypothesis can e defined as follows:

H₀: The new incentive program does not cuts down on the number of days missed by employees, i.e. d ≥ 0.

Hₐ: The new incentive program cuts down on the number of days missed by employees, i.e. d < 0.

The paired t-test would be used in this case as the data provided is a matched paired data.

The mean and standard deviation of the differences are computed in the Excel sheet.

Compute the test statistic as follows:

`t=(\bar d)/(SD/√(n))`

`=(1.10)/(1.1005/√(10))\\\\=3.161`

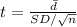
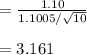
The test statistic value is 3.161.

The degrees of freedom is:

df = n - 1 = 10 - 1 = 9

Compute the p-value of the test as follows:

`p-value=P(t_(9)<3.161)=0.0058`

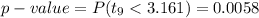
*Use a t-table.

The p-value of the test is 0.0058.

Decision rule:

If the p-value of the test is less than the significance level, 0.05, the null hypothesis will be rejected.

p-value = 0.0058 < 0.05

The null hypothesis will be rejected.

Hence, it can be concluded that the new incentive program cuts down on the number of days missed by employees.