Answer:
A. x = 0, x = -3, x = 2, and x = -2
Explanation:
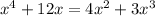
by moving the terms on the left side to the right side
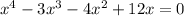
factor an
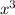 from
from
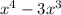
and factor - 4
 from
from
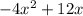
the equation becomes :
 = 0
= 0
take
 as a common factor the equation becomes :
as a common factor the equation becomes :
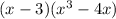 = 0
= 0
thus
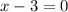 ⇒
⇒
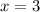
and
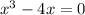 by factoring an x we get :
by factoring an x we get :
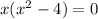 ⇒
⇒
 = 0 and
= 0 and
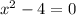
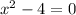 ⇒
⇒
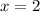 and
and

Thus
the values are :
x = 0, x = -3, x = 2, and x = -2