Question

• Solve the following differential equation xdy - ydx = 0​

Answer 1

y(x) = c_1 x

Explanation:

Solve the separable equation x ( dy(x))/( dx) - y(x) = 0:

Solve for ( dy(x))/( dx):

( dy(x))/( dx) = y(x)/x

Divide both sides by y(x):

(( dy(x))/( dx))/y(x) = 1/x

Integrate both sides with respect to x:

integral(( dy(x))/( dx))/y(x) dx = integral1/x dx

Evaluate the integrals:

log(y(x)) = log(x) + c_1, where c_1 is an arbitrary constant.

Solve for y(x):

y(x) = e^(c_1) x

Simplify the arbitrary constants:

Answer: y(x) = c_1 x

Answer 2

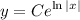`\displaystyle \largex` where C is an arbitrary constant

Explanation:

We are given the first-order ordinary differential equation:

`\displaystyle \large{xdy-ydx=0}`

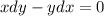
Notice that the x-term is with dy and the y-term is with dx. We can not integrate directly because x-term is supposed to be with dx and y-term is supposed to be with dy.

Therefore, move ydx to the right side via transportation property.

`\displaystyle \large{xdy =ydx}`

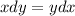
Separable Differential Equation

This method is to separate the equation in the form of f(x)dx and g(y)dy form, regardless how the equation is arranged but there must exist f(x)dx and g(y)dy.

Therefore, from the equation
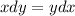`\displaystyle \large{xdy=ydx}`, divide both sides by xy.

`\displaystyle \large{(1)/(y)dy=(1)/(x)dx}`

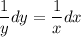
Then integrate both sides.

`\displaystyle \large{\int (1)/(y)dy=\int (1)/(x)dx}`

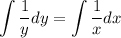
Recall the integration formula for 1/u du.

`\displaystyle \largeu`

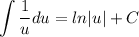
Therefore:

`\displaystyle \large+C_1`

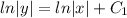
Technically, you can use this answer but I’ll simplify in y-term in case you need it.

Recall everything from logarithm conversion to exponential.

`\displaystyle \largex\\\displaystyle \large + C_1) = y\\\displaystyle \large\pm e^(C_1) \cdot e^(\ln`

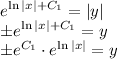
Let
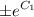`\displaystyle \large{\pm e^(C_1)}` be C then we have
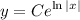`\displaystyle \largex` when C is an arbitrary constant other than 0.

When C = 0 then y becomes 0 which satisfies that dy/dx = 0 when y=0. Therefore, the solution is:

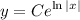`\displaystyle \large)` where C is an arbitrary constant.