Answer:
Vertically opposite angles are
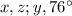
Linear pair of angles are
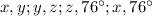
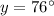 ,
,

Explanation:
Given: image
To find: vertical angles, the angles that form linear pairs, value of x, y and z
Solution:
If two lines intersect each other then the vertically angles formed are equal.
Two adjacent angles are said to be linear if their sum is
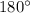 .
.
From the given image,
vertically opposite angles are
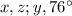
Linear pair of angles are
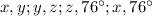
As vertically opposite angles are equal,
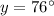
As sum of angles that form a linear pair is
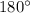 ,
,
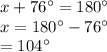
Also, as x and z are vertically opposite angles,
