Question

One of the reasons health care costs have been rising rapidly in recent years is the increasing cost of malpractice insurance for physicians. Also, fear of being sued causes doctors to run more precautionary tests (possibly unnecessary) just to make sure they are not guilty of missing something. These precautionary tests also add to health care costs. Data in the Excel Online file provided below are consistent with findings in the Reader's Digest article and can be used to estimate the proportion of physicians over the age of 55 who have been sued at least once.

Required:
a. Formulate hypotheses that can be used to see if these data can support a finding that more than half of physicians over the age of 55 have been sued at least once.
b. Use Excel or Minitab and the file LawSuit to compute the sample proportion of physicians over the age of 55 who have been sued at least once. What is the p-value for your hypothesis test?
c. At α= 0.01, what is your conclusion?

Answer 1

a) The null and alternative hypothesis are:

`H_0: \pi=0.5\\\\H_a:\pi>0.5`

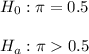
b) Sample proportion (p) = 0.6

Sample size (n) = 200

P-value = 0.0029

c) Conclusion: there is enough evidence to support the claim that the proportion of physicians over the age of 55 that have been sued at least once is significantly higher than 0.5.

Explanation:

The question is incomplete: there is no attached file with the data.

a) We want to test if more than half of the physiscians over the age of 55 have been sued at least once.

Then, the claim that will be stated in the alternative hypothesis should be that the proportion of physicians over the age of 55 that have been sued at least once is significantly higher than 0.5.

The null hypothesis should state that this proportion is not signficantly different from 0.5.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.5\\\\H_a:\pi>0.5`

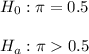
b) As we do not have the file, we will work with a sample with size n=200 and sample proportion of 0.6.

This sample proportion can be calculated from the data as

`p=x/n=120/200=0.6`

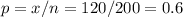
where x is the number of subjects in the sample that have been sued at least once.

The claim is that the proportion of physicians over the age of 55 that have been sued at least once is significantly higher than 0.5.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.5\\\\H_a:\pi>0.5`

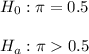
The significance level is 0.01.

The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.5*0.5)/(200)}\\\\\\ \sigma_p=√(0.00125)=0.035`

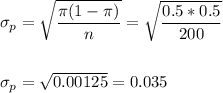
Then, we can calculate the z-statistic as:

`z=(p-\pi-0.5/n)/(\sigma_p)=(0.6-0.5-0.5/200)/(0.035)=(0.098)/(0.035)=2.758`

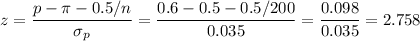
This test is a right-tailed test, so the P-value for this test is calculated as:

`\text{P-value}=P(z>2.758)=0.0029`

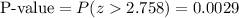
As the P-value (0.0029) is smaller than the significance level (0.01), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the proportion of physicians over the age of 55 that have been sued at least once is significantly higher than 0.5.