Question

A stone with a mass of 0.80 kgkg is attached to one end of a string 0.90 mm long. The string will break if its tension exceeds 50.0 NN. The stone is whirled in a horizontal circle on a frictionless tabletop; the other end of the string remains fixed.

(a) Draw a free-body diagram of the stone.
(b) Find the maximum speed the stone can attain without the string breaking.

Answer 1

(a) the image is attached below

(b) v = 0.237 m/s

Step-by-step explanation:

(a) The free-body diagram can be observed in the attached image

(b) To find the maximum speed you take into account the centripetal force:

`F_c=ma_c=m(v^2)/(r)`

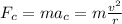
m: mass = 0.80kg

v: tangential speed of the stone = ?

r: radius of the circular trajectory of the stone = 0.90mm = 0.90*10^-3 m

The force cannot exceed 50.0N, then you have:

`50.0N=m(v^2)/(r)\\\\v=\sqrt{((50.0N)r)/(m)}=\sqrt{((50.0N)(0.90*10^(-3)m))/(0.80kg)}\\\\v=0.237(m)/(s)`

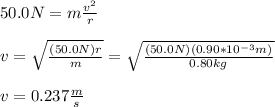
hence, the maximum speed the stone can attain without breaking the string is 0.237m/s