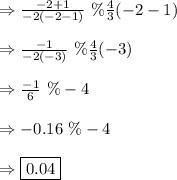Question

What is the quotient of x+1/x(x-1) % 4/3(x-1)? Assume x ≠ 0, x ≠ 1, and x ≠ −1.

Answer 1

The correct answer is B on ED 2021 Trust Me

Explanation:

Answer 2

The answer to this question can be described as follows:

when x= 2. so, quotient value= 1.12

when x=-2. so, quotient value= 0.04

Explanation:

Given:

`\bold{(x+1)/(x(x-1)) \% (4)/(3)(x-1)} \\`

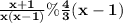
where,

`x \\eq 0, x\\eq 1 , and \ x\\eq -1`

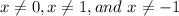
In the given question the value of x is not equal to 1, 0, and -1. so, we put the value x= 2 in the above equation:

when x= 2

`\Rightarrow (2+1)/(2(2-1)) \% (4)/(3)(2-1)\\\\\Rightarrow (3)/(2(1)) \% (4)/(3)(1)\\\\\Rightarrow (3)/(2) \% (4)/(3)\\\\\Rightarrow 1.5 \% 1.33\\\\\Rightarrow \boxed{1.12}`

when we put the value x= -2. it will give:

`\Rightarrow (-2+1)/(-2(-2-1))\ \% (4)/(3)(-2-1)\\\\\Rightarrow (-1)/(-2(-3)) \ \% (4)/(3)(-3)\\\\\Rightarrow (-1)/(6) \ \% -4 \\\\\Rightarrow -0.16\ \% -4 \\\\ \Rightarrow \boxed{0.04}`