Question

Suppose the nightly rate for a hotel in Rome is thought to be bell-shaped and symmetrical with a mean of 138 euros and a standard deviation of 6 euros. The percentage of hotels with rates between 120 and 144 euros is

Answer 1

The percentage of hotels with rates between 120 and 144 euros is 84%.

Explanation:

We know that the distribution of the nightly rate for a hotel in Rome is bell shaped with a mean of 138 euros and a standard deviation of 6 euros.

We want to know the proportion of hotels between 120 and 144 euros.

We can approximate the distribution to a normal distribution and calculate the z-score for both boundaries:

`z_1=(X_1-\mu)/(\sigma)=(120-138)/(6)=(-18)/(6)=-3\\\\\\z_2=(X_2-\mu)/(\sigma)=(144-138)/(6)=(6)/(6)=1`

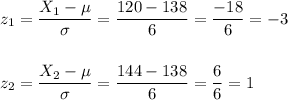
Then, we can calculate the proportion as the probability of having rates between 120 and 144:

`P=P(120<X<144)=P(-3<z<1)\\\\P=P(z<1)-P(z<-3)\\\\P=0.8413-0.0013\\\\P=0.8400`

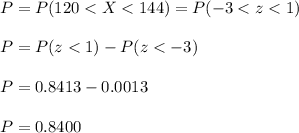
Then, we can conclude that the percentage of hotels with rates between 120 and 144 euros is 84%.