Question

Determine the maximized area of a rectangle that has a perimeter equal to 56m by creating and solving a quadratic equation. What is the length and width?

Answer 1

Area of rectangle =
`196\,m^2`

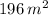
Length of rectangle = 14 m

Width of rectangle = 14 m

Explanation:

Given:

Perimeter of rectangle is 56 m

To find: the maximized area of a rectangle and the length and width

Solution:

A function
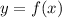`y=f(x)` has a point of maxima at
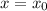`x=x_0` if
`f''(x_0)<0`

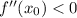
Let x, y denotes length and width of the rectangle.

Perimeter of rectangle = 2( length + width )

`=2(x+y)`

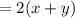
Also, perimeter of rectangle is equal to 56 m.

So,

`56=2(x+y)\\x+y=28\\y=28-x`

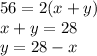
Let A denotes area of rectangle.

A = length × width

`A=xy\\=x(28-x)\\=28x-x^2`

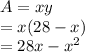
Differentiate with respect to x

`(dA)/(dx)=28-2x`

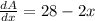
Put
`(dA)/(dx)=0`

`28-2x=0\\2x=28\\x=14`

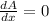
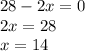
Also,

`(d^2A)/(dx^2)=-2<0`

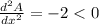
At x = 14,
`(d^2A)/(dx^2)=-2<0`

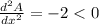
So, x = 14 is a point of maxima

So,

`y=28-x=28-14=14`

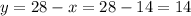
Area of rectangle:

`A=xy=14(14)=196\,m^2`

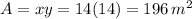
Length of rectangle = 14 m

Width of rectangle = 14 m