Given ↓
- 2 points that a line passes through
To Find ↓
- The point-slope equation for the line
Calculations ↓
First of all, we need to find the slope. In order to find the slope, we'll use the following formula :
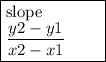
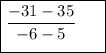

Which simplifies to :
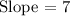
Now that we know the slope, finding the point-slope equation is a piece of cake.
Remember Point-Slope :
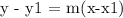
We're told to use the first point (5, 35) in our equation, so we'll do just that.


hope helpful ~