Question

DATA AND CALCULATIONS: (you must show your calculations) Part I. Determination of accuracy of a graduated cylinder Calculations: Experimental Step Measurable Mass of empty graduated cylinder 47.229 g Mass of filled graduated cylinder 71.821 g Mass of water (filled – empty) g Volume of water, calculated (calculated from mass of water, using the equation “density = mass/volume”, given the fact that the density of water is exactly 1 g/mL) mL Volume of water, measured (from the reading of the scale on the graduated cylinder) 25.0 mL Percent difference between measured and calculated volumes of water [(measured-calculated)/calculated] ×100% %

Answer 1

`\large \boxed{2 \, \%}`

Step-by-step explanation:

1. Data

Mass of graduated cylinder = 47.229 g

Mass of graduated cylinder + water = 71.821 g

Actual volume of water = 25.0 mL

2. Calculations

(a) Mass of water

Mass = 71.821 g -47.229 g = 24.592 g

(b) Volume of water

`\text{Volume} = \frac{\text{mass}}{\text{volume }} = \frac{\text{24.592 g}}{\text{ 1 g/mL}} = \text{24.592 mL}`

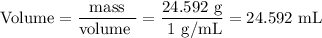
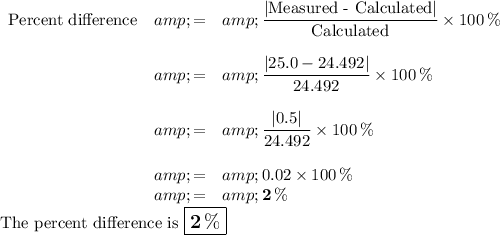
(c) Percent Difference

`\begin{array}{rcl}\text{Percent difference}&= &\frac{\lvert \text{Measured - Calculated}\lvert}{ \text{Calculated}} * 100 \,\%\\\\& = & (\lvert 25.0 - 24.492\lvert)/(24.492) * 100 \, \% \\\\& = & (\lvert 0.5\lvert)/(24.492) * 100 \, \%\\ \\& = & 0.02 * 100 \, \%\\& = & \mathbf{2 \, \%}\\\end{array}\\\text{The percent difference is $\large \boxed{\mathbf{2 \, \%} }$}`