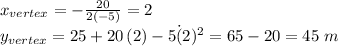Question

Example 3.4 A ball is thrown vertically

upwards with a velocity of 20 ms from
the top of a multistorey building. The
height of the point from where the ball is
thrown is 25.0 m from the ground. (a) How
high will the ball rise ? and (b) how long
will it be before the ball hits the ground?
Take g = 10 ms2

Answer 1

Maximum height reached by the ball: 45 meters from the ground

time it takes the ball to hit the ground is: 5 seconds

Step-by-step explanation:

We use the kinematic formula for accelerated motion in one dimension, understanding that the initial position of the object is 25 m (distance from the ground), the initial velocity is upward (positive) with magnitude 20 m/s, and that the acting acceleration is negative (pointing downward) the acceleration of gravity "-10 m/s".

Vertical position y of the ball (as a function of time) is:

`y= 25 +20 (t)-(10)/(2) (t)^2\\y=25+20\,t-5\,t^2`

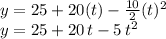
We can estimate when the ball reaches the ground (y=0) by solving for t in the quadratic equation above,

`y=25+20\,t-5\,t^2\\0=25+20\,t-5\,t^2\\0=5\, (5+4t-t^2)\\0=5\,(5+5t-t-t^2)\\0=5\,(5\,(1+t)-t(1+t))\\0=5\,(1+t)(5-t)`

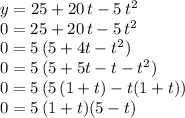
That renders two solutions: t=5 seconds, or t= -1 seconds. We select the first one (t = 5 s) since a negative time has no meaning here. This is the time it takes to reach the ground.

For the maximum height the ball reaches, we need to find the vertex position of the parabola with branches pointing down that the quadratic equation we studied generates, and which is given by:

`x_(vertex)=-(20)/(2(-5)) =2\\y_(vertex)= 25+20\,(2)-5\.(2)^2=65-20=45\,\,m`