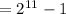Question

Let S = {1, 2, 3, ..., 12}. How many subsets of S, excluding the empty set, have an even sum but not an even product?

Answer 1

`2^(11)-1`

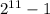
Explanation:

The set S = {1, ,2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. The total number of elements in the set (n) is 12. The sum of the elements in the set S is even if the sum of the elements of the complement of the set S is odd.

The number of pairs that can give an even sum is therefore
`2^(n-1)=2^(12-1)=2^(11)`

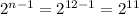
Since the empty set is excluded, The number of pairs that can give an even sum is therefore
`= 2^(11)-1`