Question

Identify the recursive formula for the sequence 20, 28, 36, 44,.

Answer 1

C.

`f_n = \left \{ {{f_1=20} \atop {f_n=f_((n-1)) + 8}; n>1} \right.`

Explanation:

Given:

Sequence: 20, 28, 36, 44,

Required

Find the recursive formula

Let
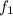`f_1` represents the first term

`f_1 = 20`

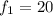
Representing the other terms in terms of the previous terms

`f_2 = 28\\f_2 = 20 +8\\f_2 = f_1 + 8`

`f_3 = 36\\f_3 = 28 + 8\\f_3 = f_2 + 8`

`f_4 = 44\\f_4 = 36 + 8\\f_4 = f_3 + 8`

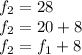
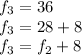
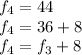
Bringing them together, we have

`f_1 = 20\\f_2 = f_1 + 8\\f_3 = f_2 + 8\\f_4 = f_3 + 8`

`f_1 = 20\\f_2 = f_(2-1) + 8\\f_3 = f_(3-1) + 8\\f_4 = f_(4-1) + 8`

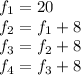
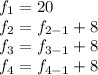
Replace each term with n

`f_1 = 20\\f_n = f_(n-1) + 8\\f_n = f_(n-1) + 8\\f_n = f_(n-1) + 8\\Where\\n > 1`

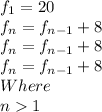
Delete repetition

`f_1 = 20\\f_n = f_(n-1) + 8\\Where\\n > 1`

So, the recursive formula is:

`f_n = \left \{ {{f_1=20} \atop {f_n=f_((n-1)) + 8}; n>1} \right.`