Answer:
A. r!
Explanation:
Combinations formula:
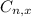 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
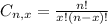
Permutations formula:
The number of possible permutations of x elements from a set of n elements is given by the following formula:
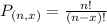
Permutation of n things taken r at a time
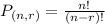
Combination of n things taken r at a time:
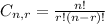
Division:
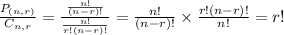
So the correct answer is:
A. r!