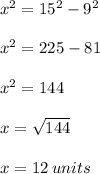Question

Which expression helps you find the length x of a side of a rectangle that has a

diagonal of 15 units and a width of 9 units?

Answer 1

`x^(2) =15^(2) -9^(2)`

Explanation:

`l^(2) + w^(2) =d^(2)`

`l^(2) + 9^(2) =15^(2)`

`l^(2) =15^(2) -9^(2)`

Answer 2

`x^2 = 15^2 - 9^2`

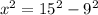
Explanation:

So we are given a rectangle whose width is 9 units, length is x units, and diagonal is 15 units.

Let us draw a diagram based on the above information.

Refer to the attached diagram, as you can notice there is a right angled triangle which means we can apply Pythagorean theorem to find out the value of unknown side x.

Recall that Pythagorean theorem is given by

`$c^2 = a^2 + b^2$`

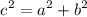
From the diagram, we have

c = 15

a = 9

b = x

So the equation becomes,

`$15^2 = 9^2 + x^2$`

`x^2 = 15^2 - 9^2`

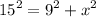
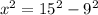
So this the correct equation!

Bonus:

The value of length x is

`x^2 = 15^2 - 9^2 \\\\x^2 = 225 - 81 \\\\x^2 = 144\\\\x = √(144)\\\\x = 12 \: units`