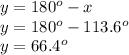An angle measures 47.2° less than the measure of its supplementary angle. What is the measure of each angle? on ixl

Question

asked Nov 3, 2021 180k views

1 Answer

Sulimmesh · Answer 1 · 2021-11-09T16:59:11+0000

Answer:

The measure of one angle is
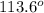113.6^o , and the measure of the other one is
66.4^o

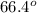
Explanation:

Recall that supplementary angles are those whose addition renders
180^o

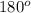
We need to find the measure of two such angles whose difference is precisely
47.2^o .

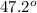Let's call such angles x and y, and consider that angle x is larger than angle y, so we can setup the following system of equations:

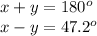
$x+y=180^o\\x-y=47.2^o$

We can now solve this by simply combining term by term both equations, thus cancelling the term in "y", and solving first for "x":

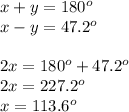
$x+y=180^o\\x-y=47.2^o\\\\2x=180^o+47.2^o\\2x=227.2^o\\x=113.6^o$

So, now we have the answer for one of the angles (x), and can use either equation from the system to find the measure of angle "y":

$y=180^o-x\\y=180^o-113.6^o\\y=66.4^o$