Question

Find the distance between the points X and Y shown in the figure.

Answer 1

`√(221)`

Explanation:

Using the distance formula:

`d=√((8-(-6))^2+(3-(-2))^2)=√(14^2+5^2)=√(196+25)=√(221)`

Hope this helps!

Answer 2

`√(221)`

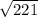
Explanation:

The distance formula is:

`d = √((x_2 - x_1)^2 + (y_2-y_1)^2)`

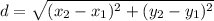
where (x1, y1) are the coordinates of the first point, and (x2,y2) are the coordinates of the second point.

The point X is at (-6,3). The point Y is at (8, -2). Therefore, we can plug these points into the formula.

`d = √((8 - (-6))^2 + (-2-3)^2)`

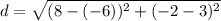
First, solve inside the parentheses

`d = √((8+6)^2 + (-2-3)^2)`

`d = √((14)^2 + (-5)^2)`

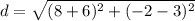
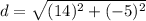
Solve the exponents.

14^2=14*14=196

`d=√(196+(-5)^2)`

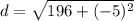
-5^2=-5*-5=25

`d=√(196+25)`

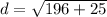
Add 196 and 25

`d=√(221)`

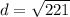
d=14.8660687473

The distance between the points is
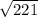`√(221)` or about 14.87