Question

Rafeeq bought a field in the form of a quadrilateral (ABCD)whose sides taken in order are respectively equal to 192m, 576m,228m,and 480m and has a diagonal equal to 672m.

a.Find its area to nearest square metre.
 b.The cost of 1 meter square land is equal to 200AED,how much did he spend to buy the field.
c.The cost of fencing 1m is equal to 12.50AED,how much did he spend to fence the field.

Answer 1

a. 85974 m²

b. 17,194,800 AED

c. 18,450 AED

Explanation:

The sides of the quadrilateral are given as follows;

AB = 192 m

BC = 576 m

CD = 228 m

DA = 480 m

Length of a diagonal AC = 672 m

a. We note that the area of the quadrilateral consists of the area of the two triangles (ΔABC and ΔACD) formed on opposite sides of the diagonal

The semi-perimeter, s₁, of ΔABC is found as follows;

s₁ = (AB + BC + AC)/2 = (192 + 576 + 672)/2 = 1440/2 = 720

The area, A₁, of ΔABC is given as follows;

`Area\, of \, \Delta ABC = √(s_1\cdot (s_1 - AB)\cdot (s_1-BC)\cdot (s_1 - AC))`

`Area\, of \, \Delta ABC = √(720 * (720 - 192)* (720-576)* (720 - 672))`

`Area\, of \, \Delta ABC = √(720 * 528 * 144 * 48)` = 6912·√(55) m²

Similarly, area, A₂, of ΔACD is given as follows;

`Area\, of \, \Delta ACD= √(s_2\cdot (s_2 - AC)\cdot (s_2-CD)\cdot (s_2 - DA))`

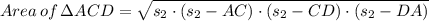
The semi-perimeter, s₂, of ΔABC is found as follows;

s₂ = (AC + CD + D)/2 = (672 + 228 + 480)/2 = 690 m

We therefore have;

`Area\, of \, \Delta ACD = √(690 * (690 - 672)* (690 -228)* (690 - 480))`

`Area\, of \, \Delta ACD = √(690 * 18* 462* 210) = √(1204988400) = 1260\cdot √(759) \ m^2`

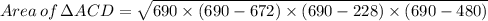
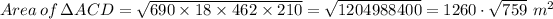
Therefore, the area of the quadrilateral ABCD = A₁ + A₂ = 6912×√(55) + 1260·√(759) = 85973.71 m² ≈ 85974 m² to the nearest meter square

b. Whereby the cost of 1 meter square land = 200 AED, we have;

Total cost of the land = 200 × 85974 = 17,194,800 AED

c. Whereby the cost of fencing 1 m = 12.50 AED, we have;

Total perimeter of the land = 576 + 192 + 480 + 228 = 1,476 m

The total cost of the fencing the land = 12.5 × 1476 = 18,450 AED