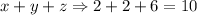Answer:
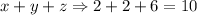
Explanation:
First we have to factor the equation:

The commom factor of first three terms and
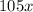 is
is
 . Note that
. Note that
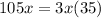
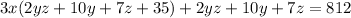
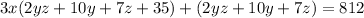
In order to have two equal factors add 35 both sides:

Let's factor
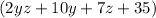
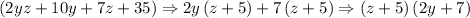
Now we have:
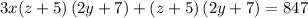
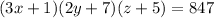
Now it is the interesting part: You have to figure out that 3 numbers multiplied by each other will result in 847.
We have
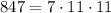
Let's try
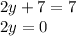
I will stop right here. This is not true.
Let's try then
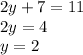
Now let's try
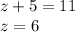
Now let's try
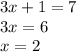
Note that in this case I didn't considered
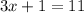 because it would not be an integer.
because it would not be an integer.
Therefore,