Answer:
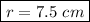
Explanation:
If M is the midpoint so AM = BM = AB/2 = 12 / 2 = 6 cm
Let's Consider a ΔOMB which would be a right angled triangle. So, We can use Pythagorean theorem to find the radius of the circle:
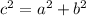
Where c is hypotenuse (radius) , a is base ( MB = 6 cm ) , b is the perpendicular (OM = 4.5 cm)
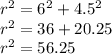
Taking sqrt on both sides
r ≈ 7.5 cm