Question

The length of rectangle B is 25% greater than the length of rectangle A. The width of rectangle B is 3/5 X the width of rectangle A. Find the fraction Area of B/Area of A Give your answer in its simplest form.

Answer 1

The value of Area of B/Area of A is 0.75.

Explanation:

It is provided that:

• The length of rectangle B is 25% greater than the length of rectangle A.
• The width of rectangle B is 3/5 X the width of rectangle A.

Consider the diagram below.

The area of a rectangle is:

`\text{Area}=\text{Length}* \text{Breadth}`

Compute the area of rectangle A as follows:

`\text{Area of A}=l* b`

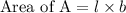
Compute the area of rectangle B as follows:

`\text{Area of B}=1.25\ l* (3)/(5)\ b=0.75\ (l* b)`

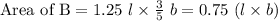
Compute the value of Area of B/Area of A as follows:

`\frac{\text{Area of B}}{\text{Area of A}}=(0.75\ (l* b))/(l* b)=0.75`

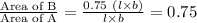
Thus, the value of Area of B/Area of A is 0.75.