Question

A circle has a diameter of 26 unites. What would be the Area of the circle, round to the nearest hundredth

Answer 1

530.93 units^2

Explanation:

The area of a circle can be found using the following formula.

`a=\pi r^2`

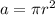
First, we must find the radius. The radius is always half of the diameter, or

r=d/2

We know that the diameter is 26 units. Therefore, we can substitute 26 in for d.

r=26/2

r=13

The radius is 13 units.

Now we know the radius. Substitute 13 in for r in the area formula.

`a=\pi r^2`

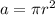
r=13

`a=\pi 13^2`

Evaluate the exponent. 13^2 is equal to 13*13, which is equal to 169.

`a=\pi *169`

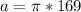
Multiply pi and 169.

a=530.929158457

Round to the nearest hundredth. The 9 in the thousandth place indicates the 2 in the hundredth place should be rounded up to a 3.

a=530.93

Add appropriate units. IN this case, the units are units^2.

a=530.93 units^2

The area of the circle is about 530.93 units^2.

Answer 2

530.93 units squared

Explanation:

The formula for the area of a circle is
`A=\pi r^(2)`. Based on this, we must plug in the given values.

The diameter is always doubled the value of the radius. Therefore, in order to find the value of the radius (r), divide it by 2. This would give us a radius of 13 units; now we have all the values to plug into the formula