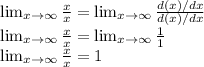Answer:
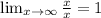
Calculating the limit by product rule is WRONG
Explanation:
Indeterminate Forms:
Indeterminate forms is an expression involving 2 functions whose limit cannot be determined by limits of individual functions. If we calculate the limits by general rules used for calculating the limits, we will not have a clear answer.
Examples of indeterminate forms are:
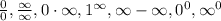
To find the limits of such forms, we have to use L'hospital rule, which states that if:
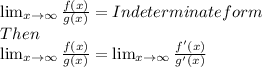
Solve the question:
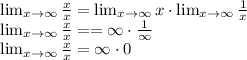
As it is an INDETERMINATE FORM, we cannot calculate its limit by product rule. We have to use L'Hospital Rule: