Question

Two functions are defined as shown.

f(x) = f(x) equals negative StartFraction 1 Over 2 EndFraction x minus 2. x – 2

g(x) = –1

Which graph shows the input value for which f(x) = g(x)?

A coordinate grid with two lines. One line labeled f(x) passes through (negative 2, 3), (0, 1), and point (2, negative 1). The second line is labeled g(x) and passes through (negative 3, negative 1), (0, negative 1), and point (3, negative 1).

A coordinate grid with two lines. One line labeled f(x) passes through (negative 4, 0), point (negative 2, 0), and (0, negative 2). The second line is labeled g(x) and passes through (negative 3, negative 1), (0, negative 1), and point (3, negative 1).

A coordinate grid with two lines. One line labeled f(x) passes through (negative 4, 1), (negative 2, 0), and point (1.5, negative 1). The second line is labeled g(x) and passes through (negative 3, negative 1), (0, negative 1), and point (1.5, negative 1).

A coordinate grid with two lines. One line labeled f(x) passes through (negative 4, 2), (negative 2, 0), and point (negative 1, negative 1). The second line is labeled g(x) and passes through (negative 3, negative 1), (negative 1, negative 1), and (1, negative 1).

Answer 1

the answer is the second graph

Explanation:

just did the test, hope this helps <3

Answer 2

Graph (2).

Explanation:

Given question is incomplete: Find the complete question in the attachment.

Given : f(x) = -
`(1)/(2)x-2`

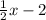
g(x) = - 1

To find : The graph showing f(x) = g(x)

If the given functions f(x) = g(x)

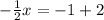
`-(1)/(2)x-2=-1`

`-(1)/(2)x=-1+2`

`-(1)/(2)x` = 1

x = -2

That means both the functions have the same value at x = -2

f(-2) = g(-2) = -1

In other words, both the lines will intersect at a point (-2, -1).

From the given graphs,

Graph number (2) shows the required results.

A straight line g(x) = -1 parallel to x- axis and another straight line f(x) =
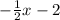`-(1)/(2)x-2`, intersect each other at (-2, -1).

Therefore, Graph (2) will be the answer.