Answer:
T = 153.72 N
Step-by-step explanation:
For this exercise we must use the conditions of translational and rotational equilibrium.
Let's set a frame of reference on the hinge, start by writing the rotational equilibrium relationship, suppose counterclockwise rotation is positive
We look for the components of the cable tension with trigonometry
cos 37 = Tₓ / T
sin 37 =
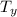 / T
/ T
Tₓ = T cos 37
T_{y} = T sin 37
the expression for rotational equilibrium is
T_{y} L + Tₓ 0 - W L / 2 - W_light 0.55 = 0
where L is the length L= 1.8 m,
T_{y} = (W L/2 + W_lght 0.55) / L
T sin 37 = Mg /2 + m_light g 0.55 / L
T = (M / 2 + m_light 0.55 / L) g / sin 35
let's calculate
T = (15/2 + 4.9 0.55 / 1.8) 9.8 / sin 35
T = 153.72 N