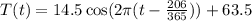Answer:
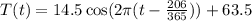
Explanation:
The temperature peaks around july26 at 78°F, and has its minimum half year later at 49°F. Assuming a year is exactly 365 days, July 26 is 206/365 of a year after January 1.
Find the formula of the trigonometric function that models the daily low temperature T in Guangzhou t years after January 1, 2015. Define the function using radians
The function can be written as ...
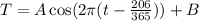
where A is half the difference of the high and low temperature values, and B is the average of the high and low temperature values.
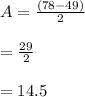
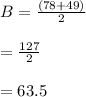
The value 206/365 is the horizontal right shift of the peak of the function. That makes the peak occur on July 26, as required.
Filling in these values gives us the function ...