Explanation:
1) The area of rectangle is ( 30x²y + 20xy ) cm² and its breadth is 10xy cm .Find its length....
= Solution ,
Length ( L ) = ?
breadth ( b ) = 10xy cm
area ( a ) = ( 30x² + 20xy )
Now ,
area ( a ) = l × b
or, ( 30x²y + 20xy ) = L × 10xy cm
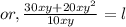
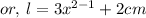
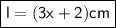
2) Subtract the quotient when 20x⁴y² is divided by 5x³y from the product of 2x and 3y.
= Solution,
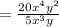
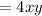
The product of 3x and 4y = 6xy
= 6x - 4xy

hope it helped !!!!