Answer:
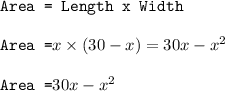
Area, A(x) = 30x - x² , as a function of the length (x).
Explanation:
Creative Landscaping has 60 yard of fencing with which to enclose a rectangular garden.
If the garden is X yards long, express the Gardens area as a function of length
Let x be the length of garden
So perimeter of rectangle = 60 yard
Perimeter = 2 * ( Length + width)
60 = 2 * ( x + width)
Width = 60/2 - x
Width= 30 - x
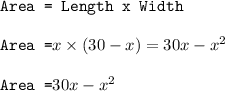
Area, A(x) = 30x - x² , as a function of the length (x).