Answer:
Approximately
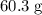 .
.
Step-by-step explanation:
Look up the relative atomic mass of
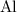 and
and
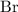 on a modern periodic table:
on a modern periodic table:
Calculate the formula mass of
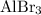 and
and
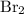 :
:
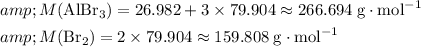 .
.
Calculate the number of moles of formula units in
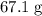 of
of
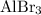 :
:
 .
.
Refer to the balanced equation for this reaction. The ratio between the coefficients of
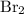 and
and
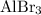 in that equation is three-to-two. That corresponds to the ratio:
in that equation is three-to-two. That corresponds to the ratio:
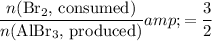 .
.
It is already calculated that approximately
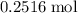 of
of
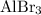 was produced through this reaction. Apply this ratio to approximate the (minimum) number of moles of
was produced through this reaction. Apply this ratio to approximate the (minimum) number of moles of
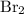 that is consumed:
that is consumed:
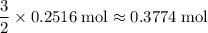 .
.
Calculate the mass of that
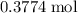 of
of
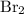 :
:
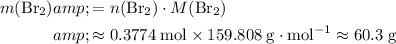 .
.