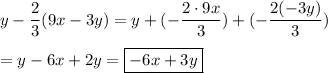Question

Expand and simplify:

a) -1/3{6(p+q)-3[p-2(p-3q)]}
A=-3p+4q

b) y-2/3(9x-3y)
A=-6x+3y

(The answer is written at the back of our books but I am struggling with the working I mean how to achieve the answer?)

Answer 1

a) -3p +4q

b) -6x +3y

Explanation:

Use the distributive property to eliminate parentheses. Use the properties of arithmetic to combine the numbers.

__

a)

The order of operations tells you to start with the inner parentheses and work outward.

`-(1)/(3)(6(p+q)-3(p-2(p-3q)))=-(1)/(3)(6(p+q)-3(p+(-2)(p) +(-2)(-3q)))\\\\=-(1)/(3)(6(p+q)-3(p-2p+6q))=-(1)/(3)(6(p+q)-3(-p+6q))\\\\=-(1)/(3)((6)(p)+(6)(q)+(-3)(-p)+(-3)(6q))=-(1)/(3)(6p+6q+3p-18q)\\\\=-(1)/(3)(9p -12q)=(-(9p)/(3))+(-(-12q)/(3))=\boxed{-3p+4q}`

__

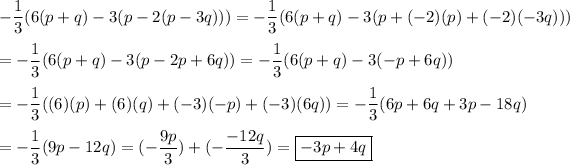
b)

Same deal for the second expression: use the distributive property and combine like terms.

`y-(2)/(3)(9x-3y)=y+(-(2\cdot9x)/(3))+(-(2(-3y))/(3))\\\\=y-6x+2y=\boxed{-6x+3y}`