Question

The graph of an absolute value function has a

vertex at (-2,3) and passes through the point (-1,
0). Using transformations of the parent function,
has the graph been dilated by a scale factor other
than 1? Explain

Answer 1

edge answer

Explanation:

Yes, the graph has been dilated.

Using the standard form of the equation, substitute in the values: h = –2, k = 3, x = –1, and y = 0.

Solve the equation to get a = –3.

Graphically, the parent function follows the pattern of right 1, up 1. Moving 1 unit to the right from the vertex, you can move down 3 units to get to the point (–1, 0), so it has been horizontally compressed.

Answer 2

Yes. The graph of the parent function has been dilated by a scale factor other than 1.

Explanation:

Let the parent function of the absolute value function is,

f(x) = |x|

This function passes through (0, 0) and slope = 1 or -1.

After transformation vertex (0, 0) becomes (-2, 3) and a point through which this function passes through is (-1, 0)

Slope of the function =
`(3-0)/(-2+1)`

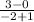
= -3

Since slope of the transformed function is less than the parent function. (-3 < -1)

Therefore, parent function will be dilated by a scale factor other than 1.