Question

The set of points (-3, 4), (-1, 1), (-3,-2), and (-5,1) identifies the vertices of a quadrilateral. Which is the most specific description to tell which figure the points form?

parallelogram
please help
​

Answer 1

Option (4). Rhombus

Explanation:

From the figure attached,

Distance AB =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

=
`√((1-4)^2+(-5+3)^2)`

=
`√((-3)^2+(-2)^2)`

=
`√(13)`

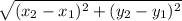
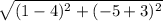
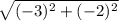
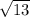
Distance BC =
`√((4-1)^2+(-3+1)^2)`

=
`√(9+4)`

=
`√(13)`

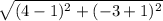
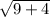
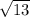
Distance CD =
`√((-2-1)^2+(-3+1)^2)`

=
`√(9+4)`

=
`√(13)`

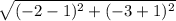
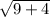
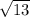
Distance AD =
`√((1+2)^2+(-5+3)^2)`

=
`√(9+4)`

=
`√(13)`

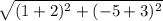
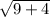
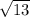
Slope of AB (
`m_(1)`) =
`(y_(2)-y_(1))/(x_(2)-x_(1))`

=
`(4-1)/(-3+5)`

=
`(3)/(2)`

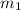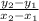
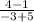
Slope of BC (
`m_(2)`) =
`(4-1)/(-3+1)`

=
`-(3)/(2)`

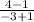
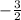
If AB and BC are perpendicular then,

`m_(1)* m_(2)=-1`

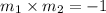
But it's not true.

[
`m_(1)* m_(2)=((3)/(2))(-(3)/(2))` = -
`(9)/(4)`]

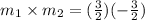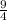It shows that the consecutive sides of the quadrilateral are not perpendicular.

Therefore, ABCD is neither square nor a rectangle.

Slope of diagonal BD =
`(4+2)/(-3+3)`

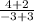
= Not defined (parallel to y-axis)

Slope of diagonal AC =
`(1-1)/(-1+5)`

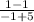
= 0 [parallel to x-axis]

Therefore, both the diagonals AC and BD will be perpendicular.

And the quadrilateral formed by the given points will be a rhombus.