Answer:
Explanation:
I am taking q as some integer.
Let a be the positive integer.
And, b = 4 .
Then by Euclid's division lemma,
We can write
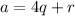 ,for some integer
,for some integer
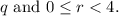
°•° Then, possible values of r is 0, 1, 2, 3 .
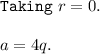
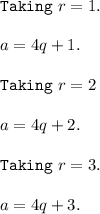
But a is an odd positive integer, so a can't be 4q , or 4q + 2
[ As these are even ] .
•°• a can be of the form 4q + 1 or 4q + 3 for some integer q .