Question

Question 2 Multiple Choice Worth 5 points)

(06.04 MC)
The figure below shows
shaded circular region inside a larger circle:
r2 inches
R = 5 inches
What is the probability that a point chosen inside the larger circle
not in the shaded region?
O 84%
O 50%
42%
o o
O 16%

Answer 1

Probability that point chosen is in large circle but not in shaded region:

P = 84%

Explanation:

Given that

r = 2 inches

R = 5 inches

Area of Small circle (shaded region):

`A=\pi{r}^2\\A=\pi(2)^2\\A=12.56 in^2`

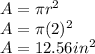
Area of Large circle:

`A=\pi{r}^2\\A=\pi(5)^2\\A=78.5in^2`

Probability of Point being chosen is inside shaded region:

`P=(12.56)/(78.5)\\P=0.16\\P=16\%`

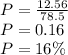
Probability of Point being chosen is NOT inside shaded region:

P = 100% - 16%

P = 84%