Answer:
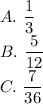
Explanation:
Total outcomes possible: 36
A. Divisible by 3
Possible options are:
3, 6, 9 and 12.
Possible outcomes for 3 are: {(1,2), (2,1)} Count 2
Possible outcomes for 6 are: {(1,5), (2,4), (3,3), (5,1),(4,2)} Count 5
Possible outcomes for 9 are: {(3,6), (4,5), (5,4),(6,3)} Count 4
Possible outcomes for 12 are: {(6,6)} Count 1
Total count = 2 + 5 + 4 + 1 = 12
Probability of an event E can be formulated as:
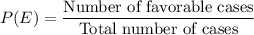

B. Less than 7:
Possible sum can be 2, 3, 4, 5, 6
Possible cases for sum 2: {(1,1)} Count 1
Possible cases for sum 3: {(1,2), (2,1)} Count 2
Possible cases for sum 4: {(1,3), (3,1), (2,2)} Count 3
Possible cases for sum 5: {(1,4), (2,3), (3,2),(4,1)} Count 4
Possible cases for sum 6: {(1,5), (2,4), (3,3), (5,1),(4,2)} Count 5
Total count = 1 + 2 + 3 + 4 + 5 = 15
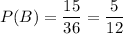
C. Divisible by 3 and less than 7:
Here, common cases are:
Possible outcomes for 3 are: {(1,2), (2,1)} Count 2
Possible outcomes for 6 are: {(1,5), (2,4), (3,3), (5,1),(4,2)} Count 5
