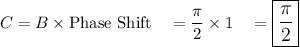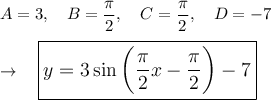Question

The graph of a sinusoidal function has a minimum point at (0, - 10) and then has a maximum point at (2, - 4) Write the formula of the function , where x is entered in radians .

Answer 1

Answer:
`\bold{y=3sin\bigg((\pi)/(2)x-(\pi)/(2)\bigg)-7}`

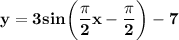
Explanation:

Minimum: (0, -10)

Maximum: (2, -4)

y = A sin (Bx - C) + D

• Amplitude (A) = (Max - Min)/2
• Period = 2π/B → B = 2π/Period
• Phase Shift = C/B → C = B × Phase Shift
• Midline (D) = (Max + Min)/2

`A=(-4-(-10))/(2)\quad =(-4+10)/(2)\quad =(6)/(2)\quad =\large\boxed{3}`

`\text{x-value of Max minus x-value of Min}= (1)/(2)\text{Period}\\\\2 - 0 = (1)/(2)P\quad \rightarrow \quad P=4\\\\\\B=(2\pi)/(P)\quad =(2\pi)/(4)\quad =\large\boxed{(\pi)/(2)}\\`

`D = \frac{\text{Max + Min}}{2}\quad = (-4+(-10))/(2)\quad =(-14)/(2)\quad =\large\boxed{-7}`

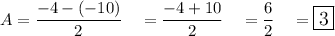
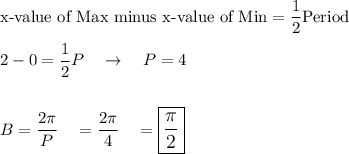
Sin usually starts at (0, 0). For this graph, the midline touches 0 when x = 1 so the Phase Shift = 1.

`C = B * \text{Phase Shift}\quad = (\pi)/(2)* 1\quad =\large\boxed{(\pi)/(2)}`

`A=3, \quad B=(\pi)/(2), \quad C=(\pi)/(2),\quad D=-7\\\\\rightarrow \quad \large\boxed{y=3\sin \bigg((\pi)/(2)x-(\pi)/(2)\bigg)-7}`