Question

The cone in Fig. 15.29 is exactly half full of water

by volume. How deep is the water in the cone?

​

Answer 1

Since this cone is exactly half full of water by volume, the depth of the water in the cone is 12.70 cm.

In Mathematics and Euclidean Geometry, the volume of a cone can be calculated by using this formula:

V = 1/3 × π
`r^2`h

Where:

• V represents the volume of a cone.
• h represents the height.
• r represents the radius.

Note: Radius = diameter/2

Radius = 12/2 = 6 cm.

Substituting the given parameters into the volume of a cone formula, we have the following;

Volume of cone, V = 1/3 × 3.14 ×
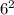`6^2` × 16

Volume of cone, V = 603.88 cubic cm.

Since the cone is exactly half full of water by volume, we have:

Volume of water = 603.88/2

Volume of water = 301.44 cubic cm.

The ratio of the radius to the height when half full of water is given by;

r/h = 6/16

r = 6h/16 cm.

Now, we can determine the height or depth of the water in this cone;

301.44 = 1/3 × 3.14 ×
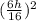`((6h)/(16) )^2` × h

301.44 = 0.1471875
`h^3`

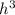
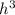`h^3` = 301.44/0.1471875

`h=\sqrt[3]{2048}`

Depth, h = 12.6992 ≈ 12.70 cm.

Answer 2

The water is 8 cm deep.

Explanation:

In order to solve this problem we first need to find the total volume of the cone, this is done by using the following formula:

`V = (\pi*r^2*h)/(3)\\\\V = (\pi*(6)^2*16)/(3)\\\\V = (576*\pi)/(3)\\\\V = 192*\pi`

The total volume of the cone is 192*pi cm³, if it is half full then the volume of the water is half of that, which would be 96*pi cm³, we can apply this value to the same formula in order to find the height of the water:

`96\pi = (\pi*(6)^2*h)/(3)\\\\\pi*36*h = 288\pi\\h = (288)/(36)\\h = 8 \text{ cm}`

The water is 8 cm deep.