Question

a total of 38,000 is invested in two municipal bonds that pay 4.75% and 5.25% simple interest. The investor wants an annual interest income of $1925 from the investments. What amount should be invested in the 4.75% bond?

Answer 1

$14,000 should be invested in the 4.75% bond

Explanation:

We need to find the "x" amount to be invested at 4.75%.

Note also that the total amount to be invested is $38,000, and therefore what will be invested in the other bond (5.25 percent) must be "$38,000-x"

We are now writing the equation for adding both interests from this investment, recalling the formula for simple interest such as: I = P * r * t

Where I care = Interest

P = principal (deposited amount)

R = rate of percent in decimal form

T = One Year Time

So for the x amount of the 4.75 percent bond the interest would be after one year:

For the amount ($38000-x on the 5.25 percent bond, the interest would be: after a year

Adding both interests would then render:

Now, remember that the investor wants that total interest to be $1925, then we can write and solve the following equation for "x"

Answer 2

$14,000 should be invested in the 4.75% bond

Explanation:

We need to find the amount "x" that needs to be invested at 4.75%.

Notice as well that the total to be invested equals $38,000, and therefore, what is going to be invested in the other bond (5.25%) must be "$38,000-x"

We now write the equation for the addition of both interests coming from such investment, recalling the formula for simple interest as : I = P * r * t

Where I = Interest

P = Principal (amount deposited)

r = percent rate in decimal form

t = time (one year)

so for the amount x on the 4.75% bond, the interest after one year would be:

`I_1=x\,*\,0.0475\,*\,1=0.0475\,x`

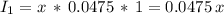
For the amount ($38000-x on the 5.25% bond, the interest after one year would be:

`I_2=(38000-x)\,*\,0.0525\,*\,1=1995-0.0525\,x`

Then, the addition of both interests would render:

`I_1+I_2=0.0475\,x+1995-0.0525\,x=1995-0.005\,x`

Now, recall that the investor wants this total interest to be $1925, then we can write the following equation and solve for "x":

`1995-0.005\,x=1925\\1995-1925=0.005\,x\\70=0.005\,x\\x=70/0.005\\x=14000`

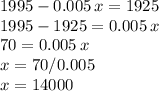
Therefore, the amount to be deposited in the 4.75% bond should be $14,000