Answer:
Step-by-step explanation:
Given that:
number of moles of super cooled liquid water = 1
Melting enthalpy of ice = 6020 J/mol
Freezing point =0 °C = (0 + 273 K)= 273 K
The decrease in entropy of the system during freezing for 1 mol (i.e during transformation from liquid water to solid ice ) = - 6020 J/mol × 1 mol /273 K = -22.051 J/K
Entropy change during further cooling from 0 °C (273 K) to -10 °C (263 K)
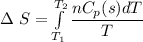
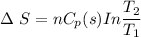
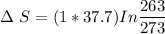
Δ S = -1.4 J/K
Total entropy change of the system = - 22.05 J/K - 1.4 J/K = - 23.45 J/K
Entropy change of universe = entropy change of the system+ entropy change of the surrounding
According to the second law of thermodynamics
Entropy change of universe >0
SO,
Entropy change of the system + entropy change in the surrounding > 0
Entropy change in the surrounding > - entropy change of the system
Entropy change in the surrounding > - (- 23.53 J/K)
Entropy change in the surrounding > 23.53 J/K
b) Make some comments on entropy changes from the obtained data.
From the data obtained; we will realize that the entropy of the system decreases as cooling takes place when water is be convert to ice , randomness of these molecules reduces and as cooling proceeds , hence, entropy reduces more as well and the liberated heat will go into the surrounding due to this entropy of the surrounding increasing.