Question

A publisher reports that 41% of their readers own a laptop. A marketing executive wants to test the claim that the percentage is actually less than the reported percentage. A random sample of 320 found that 36% of the readers owned a laptop. Is there sufficient evidence at the 0.05 level to support the executive's claim? Find the value of the test statistic. Round your answer to two decimal places. Specify if the test is one-tailed or two-tailed. Determine the decision rule for rejecting the null hypothesis, H0. Make the decision to reject or fail to reject the null hypothesis. State the conclusion of the hypothesis test.

Step 1 of 6: State the null and alternative hypotheses.

Answer 1

Explanation:

Hello!

The objective is to test the claim that less than 41% of the publisher's readers own a laptop.

To do so, a sample of 320 readers was taken and the proportion of readers that own a laptop resulted in 36%

Be X: number of readers that own a laptop.

X~Bi(n;p)

n=320

Sample proportion p'= 0.36

The hypotheses are:

H₀: p ≥ 0.41

H₁: p < 0.41

α: 0.05

`Z=\frac{p'-p}{\sqrt{(p(1-p))/(n) } }`≈N(0;1)

`Z_(H_0)=\frac{0.36-0.41}{\sqrt{(0.41(1-0.41))/(320) } }= -1.82`

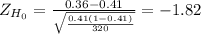
This test is one-tailed to the left, meaning, that you'll reject the null hypothesis to small values of Z, there is only one critical value that defined the rejection region:

`Z_(\alpha )= Z_(0.05)= -1.645`

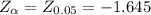
The decision rule is:

If
`Z_(H_0)` ≤ -1.645, reject the null hypothesis.

If
`Z_(H_0)` > -1.645, do not reject the null hypothesis.

The calculated value is less than the critical value, then the decision is to reject the null hypothesis.

So at a 5% significance level, the test is significant. You can conclude that the population proportion of the publisher's readers that own a laptop is less than 41%.

I hope this helps!