Question

A ladder of length 15 feet is leaning a wall

and is sliding away from the wall top of the ladder is sliding down at a rate of 3 ft/s. Find rate at which bottom of the latter is moving at the at the moment when the top ladder is 12ft from the ground

Answer 1

The rate of change of the bottom of the ladder is 4 feet per second.

Explanation:

Let be
`l` the length of the ladder,
`x` the horizontal distance from the bottom of the ladder to the wall and
`y` the vertical distance from the top of the ladder to the floor. Besides, let is assume that wall is perpendicular to floor. The geometry associated with the ladder can be modelled after the Pythagorean Theorem:

`l^(2) = x^(2) + y^(2)`

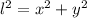
Rate of change in time experimented by the ladder is found after deriving the previous formula:

`0 = 2\cdot x \cdot \dot x + 2\cdot y \cdot \dot y`

`x\cdot \dot x + y \cdot \dot y = 0`

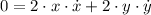
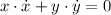
Besides,

`x = \sqrt{l^(2)-y^(2)}`

Then,

`\sqrt{l^(2)-y^(2)}\cdot \dot x + y \cdot \dot y = 0`

Now, the rate of change of the horizontal distance is cleared in the expression:

`\dot x = -\frac{y\cdot \dot y}{\sqrt{l^(2)-y^(2)}}`

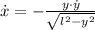
Given that
`l = 15\,ft`,
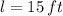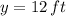`y = 12\,ft` and
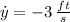`\dot y = -3\,(ft)/(s)` (as top of the ladder is sliding down), the rate of change of the bottom of the ladder is:

`\dot x = - \frac{(12\,ft)\cdot \left(-3\,(ft)/(s) \right)}{\sqrt{(15\,ft)^(2)-(12\,ft)^(2)} }`

`\dot x = 4\,(ft)/(s)`

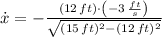
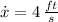
The rate of change of the bottom of the ladder is 4 feet per second.