Answer:
Those graphs do not intersect.
Estes gráficos no se intersecciónan
Explanation:
The intersection points are x for which:
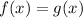
In this question:
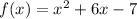
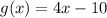
So
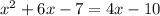
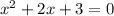
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
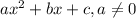 .
.
This polynomial has roots
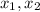 such that
such that
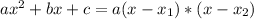 , given by the following formulas:
, given by the following formulas:
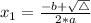
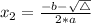

In this question:
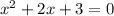
So
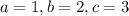
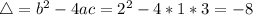
Sincce
 is negative, there are no solutions, which means that those graphs do not intersect.
is negative, there are no solutions, which means that those graphs do not intersect.