Question

Please help, need both 3 and 1, show your work if possible

Answer 1

1. The equation has 2 solutions 3. p = 0, p = -2

Explanation:

1. The quadratic equation is ax^2+bx+c=0
`x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

in the equation a = 2, b = 3 and c = 5

so the equation would be
`x_(1,\:2)=(-(-3)+ √((-3)^2-4*2*5))/(2*2)`

`x_(1,\:2)=(3+√(9-4*2*5))/(2*2)`

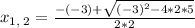
simplify

`3+√(31)i`

divide by 4

`(3)/(4) +(√(31) )/(4)i` or
`x=(-\left(-3\right)-√(\left(-3\right)^2-4\cdot \:2\cdot \:5))/(2\cdot \:2):\quad (3)/(4)-i(√(31))/(4)`

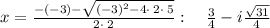
3. 4p(5p + 10) = 0 Using the Zero Factor Principle aka. zero-product property If a*b=0 then a=0 or b=0 or both a=0 and b=0

p = 0

5p + 10 = 0

subtract ten from both sides

5p = -10

divide by 5

p = -2