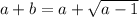Question

What is the conjugate?

a - √a-1

UREGENT PLEASE HELP

Answer 1

the conjugate of
`a -√(a-1) \ = a + √(a -1)`

Explanation:

Given;

`a - √(a-1)`

Conjugate of
`a -√(x) \ \ \ is \ \ a \ + \ √(x)`

let (a - 1) = x

a - √x = a + √x

∴
`a -√(a-1) \ = a + √(a -1)`

Therefore, the conjugate of
`a -√(a-1) \ = a + √(a -1)`

Check

`(a -√(a-1)) *(a+√(a-1) ) = a^2 + \ a√(a-1)\ - \ a√(a-1) - (a-1)\\\\(a -√(a-1)) *(a+√(a-1) ) = a^2 - (a-1)\\\\(a -√(a-1)) *(a+√(a-1) ) = a^2 -a+1`

The result is a rational number, hence
`a + √(a-1) \ \ is \ \ conjugate \ of \ \ a -√(a-1)`

Answer 2

`a+√(a-1)`

Explanation:

The conjugate of an expression of the form:

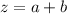`z=a+b` (1)

is another expression of the form:

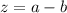`z=a-b` (2)

In the same way, if your expression is
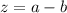`z=a-b`, the conjugate is
`z=a+b`.

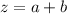You have the following expression:

`a-√(a-1)`

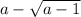
by comparing with the equations (1) and (2) you can take a=a and b=√a-1. Thus, you have the expression z = a - b. The conjugate is z = a + b. Then, you can conclude that the conjugate is:

`a+b=a+√(a-1)`